Factors of 60: Pair Factors, Prime Factors, Factor Tree, and Examples
Factors of 60 play a crucial role in understanding basic arithmetic and number theory. Have you ever wondered what these factors are and how they can be derived?
This article will delve into all the factors of 60, exploring prime factors, factor trees, and offering practical examples. By the end, you will have a comprehensive understanding of how to find and utilize the factors of 60.

Part 1: What are the Factors of 60?
Factors of 60 refer to the integers that can be multiplied together to yield the product of 60. In other words, if you can divide 60 by a number without leaving a remainder, that number is a factor of 60. Understanding factors is fundamental in mathematics, as they are used in various applications, including simplifying fractions and solving equations. The factors of 60 include both positive and negative integers.
All the factors of 60
All the factors of 60 is: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
These numbers can multiply in pairs to give 60, which is why they are referred to as pair factors. For instance:
- 1×60=60
- 2×30=60
- 3×20=60
- 4×15=60
- 5×12=60
- 6×10=6
Part 2: How to Find the Factors of 60?
Finding the factors of 60 involves identifying all the integers that can divide 60 evenly, without leaving a remainder. Understanding how to find factors of 60 is an essential skill in mathematics, as it helps in simplifying problems, especially when working with fractions or solving equations. Here’s a step-by-step process to determine the factors of a number like 60.
Steps to Find the Factors of 60
Step 1. Start with the Number 1: Begin with the smallest integer, which is 1. Since 1 can divide any number, it is always a factor.
60÷1=60
Step 2. Check Integers Up to the Square Root: The square root of 60 is approximately 7.75. Therefore, check all integers from 1 up to 7.
Step 3. Divide by Each Integer:
- Check each integer to see if it divides 60 evenly:
- 2: 60÷2=30 (Both 2 and 30 are factors)
- 3: 60÷3=20 (Both 3 and 20 are factors)
- 4: 60÷4=15 (Both 4 and 15 are factors)
- 5: 60÷5=12 (Both 5 and 12 are factors)
- 6: 60÷6=10 (Both 6 and 10 are factors)
- 7: 60÷7 does not yield an integer, so 7 is not a factor.
Step 4. Compile the List of Factors:
From the divisions above, we gather the factors: Factors found: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Step 5. Include Negative Factors:
Don’t forget to include the negative counterparts: -1, -2, -3, -4, -5, -6, -10, -12, -15, -20, -30, -60
Part 4: Prime Factorisation of 60
The prime factorization of 60 involves breaking down the number into its prime factors—the prime numbers that multiply together to form 60. Understanding the prime factors of 60 is essential in various mathematical applications, including simplifying fractions and solving equations.
To find all the prime factors, we start with the smallest prime factor and work our way up, ensuring we identify each prime number involved in the factorization.Start with the smallest prime factor: The smallest prime factor of 60 is 2.
The Procession of Calculation
| Step | Description |
|---|---|
| 1. Start with the Number | Begin with the number 60. |
| 2. Identify the Smallest Prime Factor | The smallest prime number is 2. Check if 60 is divisible by 2: 60÷2=30 Since 60 is divisible by 2, we identify 2 as a prime factor. |
| 3. Continue Factoring | Next, take 30 and divide it by 2 again: 30÷2=15 We can add another 2 to our list of prime factors. |
| 4. Factor the Next Number | Now, take 15. The next smallest prime number is 3. Check if 15 is divisible by 3: 15÷3=5 We identify 3 as another prime factor. |
| 5. Identify Remaining Prime Factor | The number 5 is also a prime number. Since we have reached 1 at the end, we cannot continue with the division method, so we stop here. |
| 6. Compile the Prime Factors of 60 | The prime factors of 60 are: 22 (occurs twice), 31, 51 |
Thus, the prime factorization of 60 can be expressed as:
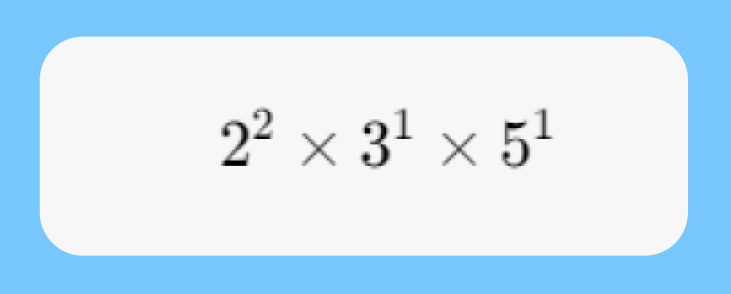
Part 4: Factor Tree of 60
A factor tree of 60 is a visual representation of the process of breaking down a number into its prime factors. factor tree of 60 are a useful tool for understanding the prime factorization of a number, which can be beneficial in various mathematical applications, such as finding the greatest common divisor or simplifying fractions. Below are the steps to create the factor tree of 60.
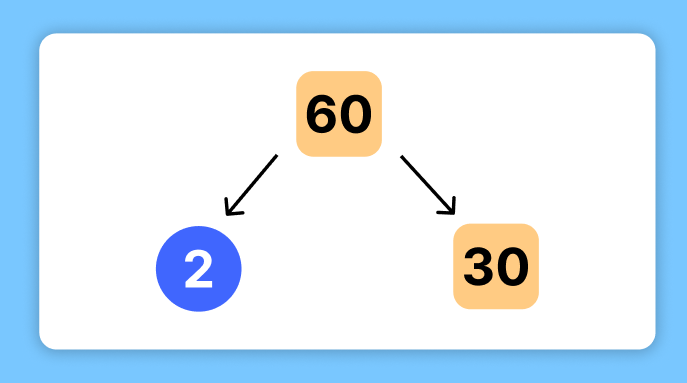
Step 1. Start with the Number: Begin with the number 60 at the top of the tree.
Step 2. Divide by the Smallest Prime Numbers
- The smallest prime number is 2. Divide 60 by 2:
- 60÷2=30
- Write 2 as a branch connected to 60, and 30 as the next level.
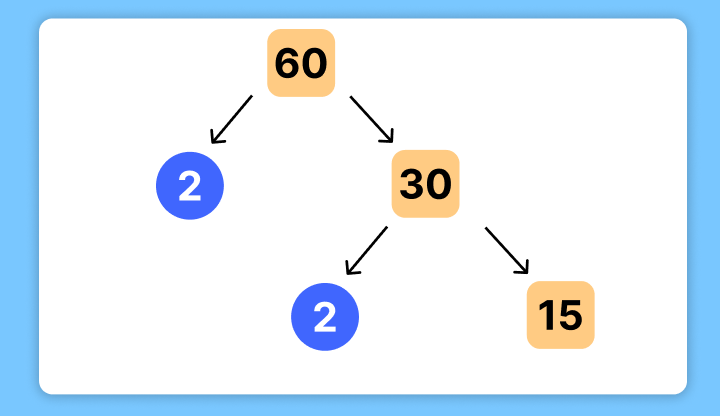
Step 3. Continue Factoring:
- Next, take 30 and divide it by the smallest prime number again:
- 30÷2=15
- Write another branch for 2, connecting it to 30, with 15 as the next level.
Step 4. Factor the Next Number:
- Now, take 15. Since 15 is not divisible by 2, try the next smallest prime, which is 3:
- 15÷3=5
- Write 3 as a branch connected to 15, with 5 as the next level.
Step 5. Identify Remaining Prime Factor:
- The number 5 is a prime number, which means it cannot be divided further.
Step 6. Complete the Factor Tree: The factor tree can now be summarized as:
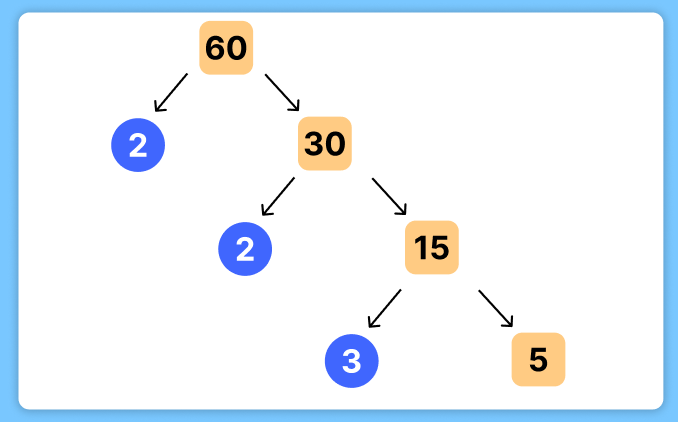
Note: The factor tree of 60 shows the prime factorization of 60 as:
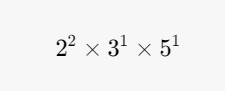
This method provides a clear and organized way to break down numbers into their prime components, enhancing your understanding of factorization.
Part 5: Pair Factors of 60
Pair factors of a number are pairs of integers that multiply together to give that number. For 60, we can identify both positive pair factor and negative pair factor. Understanding these factor pairs is useful in various mathematical contexts, such as simplifying fractions or finding common multiples. Below are the tables listing the factors of 60 along with their corresponding positive and negative pair factors.
Table 1: Positive Factor Pair of 60
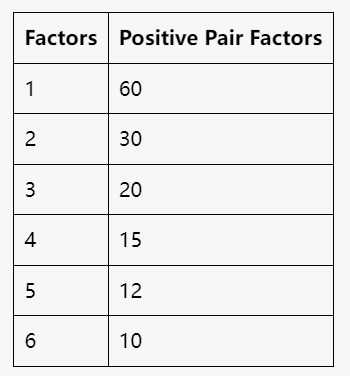
Table 2: Negative Factor Pair of 60
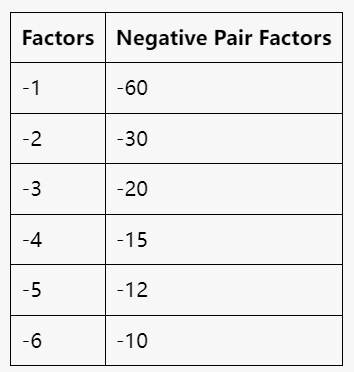
These tables illustrate the relationship between the factors of 60 and their corresponding positive factors and negative factors, along with their factor pair, enhancing our understanding of multiplication and division within this number.
Part 6: Solved Examples on Factors of 60
Understanding the factors of 60 is essential in mathematics, as it helps in various operations like simplifying fractions and solving equations. Here are five solved examples that demonstrate how to identify and use the factors of 60 effectively.
Example 1: Identify All Factors of 60
| Question: | List all the factors of 60. |
| Answer: | The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. |
| Explanation: | These numbers can be multiplied in pairs to give 60. For instance, 1×601×60, 2×302×30, etc. |
Example 2: Find Pair Factors of 60
| Question: | What are the positive pair factors of 60? |
| Answer: | The positive pair factors of 60 are: (1, 60), (2, 30), (3, 20), (4, 15), (5, 12), (6, 10). |
| Explanation: | Each pair multiplies to give 60, confirming their relationship as factor pairs. |
Example 3: Prime Factorization of 60
| Question: | What is the prime factorization of 60? |
| Answer: | The prime factorization of 60 is 22×31×51. |
| Explanation: | This is derived from breaking down 60 into its prime factors using a factor tree or successive division. |
Example 4: Find Common Factors
| Question: | What are the common factors of 60 and 30? |
| Answer: | The common factors of 60 and 30 are: 1, 2, 3, 5, 6, 10, 15, 30. |
| Explanation: | Both numbers share these factors, as they can divide evenly into both without a remainder. |
Example 5: Determine if 15 is a Factor of 60
| Question: | Is 15 a factor of 60? |
| Answer: | Yes, 15 is a factor of 60. |
| Explanation: | Since 60÷15=4 with no remainder, 15 divides evenly into 60, confirming it as a factor. |
Practice Questions on Factors of 60
Frequently Asked Question on Factors of 60
Q 1. Is 60 a composite number?
Yes, 60 is a composite number. A composite number is defined as a positive integer that has at least one positive divisor other than one and itself. Since 60 has more than two factors, such as 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30, it confirms that 60 is indeed a composite number.
Q 2. The Common Factors of 60 and 30
Additionally, when comparing two or more numbers, common factors are the factors that they share. For example, the common factors of 60 and 30 include 1, 2, 3, 5, 6, 10, 15, and 30. Identifying common factors is useful in various mathematical operations, such as finding the greatest common divisor (GCD).
Understanding both the factors of 60 and the concept of common factors provides a solid foundation for further mathematical exploration.

Q 3. All the Prime Factors of 60
The prime factors of 60 are the prime numbers that multiply together to produce 60. The complete list of prime factors of 60 is:

The prime factorization of 60 can be expressed as:
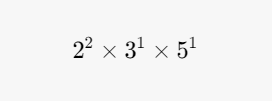
Q 4. What is the greatest common factor (GCF) of 36 and 60?
The greatest common factor (GCF) is the largest number that divides two or more integers without leaving a remainder. For 36 and 60, we start by listing their factors: the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36, while the factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. By comparing these lists, we find the common factors are 1, 2, 3, 4, 6, and 12. The largest of these common factors is 12. Therefore, the greatest common factor of 36 and 60 is 12.

Q 5. What is the greatest common factor (GCF) of 45 and 60?
The greatest common factor (GCF) is the largest number that divides two integers without leaving a remainder. For 45 and 60, we first list their factors: the factors of 45 are 1, 3, 5, 9, 15, and 45, while the factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. By comparing these, we find the common factors are 1, 3, 5, and 15. The largest of these is 15, so the greatest common factor of 45 and 60 is 15.

Q 5. What is the greatest common factor of 24 and 60?
As we know, the factors of 24 is 1, 2, 3, 4, 6, 8, 12, 24, while the factors of 60 is 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. So, the the common factors of 24 and 60 are 1, 2, 3, 4, 6, 12. Then, we can conclude that the greatest common factor from the list of common factors is 12.

Conclusion
Factors of 60 are essential for various mathematical applications and understanding their prime factors, factor trees, and pair factors is crucial. By grasping the concept of factors of 60, you equip yourself with valuable skills for solving more complex mathematical problems. Whether in school or everyday life, knowledge of factors can enhance your arithmetic capabilities significantly. If you want to know more, please click the following link.
Delvair holds a degree in Physics from the Federal University of Maranhão, Brazil. With over six years of experience, she specializes in teaching mathematics, with a particular emphasis on Math Kangaroo competitions. She firmly believes that education is the cornerstone of society’s future. Additionally, she holds the conviction that every child can learn given the right environment and guidance. In her spare time, she enjoys singing and tending to her plants.




![Math League: Competitions, Challenges, and Achievements [2025 Full Guide] Math League: Competitions, Challenges, and Achievements [2025 Full Guide]](https://wp-more.wukongedu.net/blog/wp-content/uploads/2024/01/school-2353406-520x293.jpg)




![Top 15 Summer Programs for High School Students [2025] Top 15 Summer Programs for High School Students [2025]](https://wp-more.wukongedu.net/blog/wp-content/uploads/2024/06/image-104-1-520x293.png)

Comments0
Comments