What are the Multiples of 3? [Solved Examples +List of 3 Times Table]

Have you ever wondered what multiples of 3 are and how they work? Understanding multiples is fundamental in mathematics, and knowing the multiples of 3 can help you in various mathematical applications, from basic arithmetic to more complex problems.

Multiples of a number are obtained by multiplying that number by natural numbers. For example, the multiples of 3 are generated by multiplying 3 by natural numbers like 1, 2, 3, and so on. Common multiples are numbers that are shared multiples of a given set of numbers, and finding them involves identifying the multiples that appear in all lists.

This article will provide a comprehensive overview of multiples of 3, including a detailed list of multiples, explanations through repeated addition, and solved examples. Whether you’re a student looking to enhance your math skills or an adult brushing up on basic concepts, this guide will help clarify the topic of multiples of 3, including odd numbers and the relationship between multiples of 3 and 4.

What are the Multiples of 3?

Multiples of 3 are simply the results you get when you multiply 3 by any whole number. In mathematical terms, if we denote a multiple of 3 as 3n, where n is a whole number (0, 1, 2, 3, …), then the multiples of 3 will be:

• 0 (3 × 0)
• 3 (3 × 1)
• 6 (3 × 2)
• 9 (3 × 3)
• 12 (3 × 4)
• 15 (3 × 5)
• 18 (3 × 6)
• 21 (3 × 7)
• 24 (3 × 8)
• 27 (3 × 9)
• and so on.

Numbers which leave a remainder value when divided by 3 are not considered multiples.

Each number in the sequence is a multiple of 3. The multiples of 3 can be visualized on a number line:

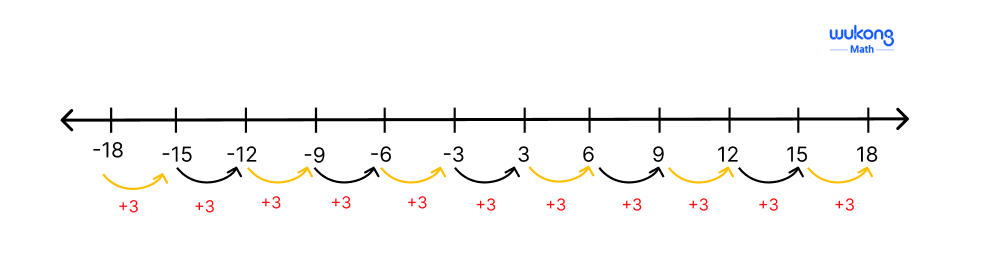
As you can see, the sequence continues indefinitely, creating an infinite list of multiples of 3. Not every multiple of 7 will appear in the list of multiples of 3, highlighting the differences between these sets of multiples.

Multiples of 3 up to 100:

0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99.

List of Multiples of 3: Times Table

Here’s the times table for the multiples of 3 from 1 to 20:

n	3 × n	Result
1	3 × 1	3
2	3 × 2	6
3	3 × 3	9
4	3 × 4	12
5	3 × 5	15
6	3 × 6	18
7	3 × 7	21
8	3 × 8	24
9	3 × 9	27
10	3 × 10	30
11	3 × 11	33
12	3 × 12	36
13	3 × 13	39
14	3 × 14	42
15	3 × 15	45
16	3 × 16	48
17	3 × 17	51
18	3 × 18	54
19	3 × 19	57
20	3 × 20	60

Specific multiples can be highlighted in larger bold for emphasis.

This table provides the first 20 multiples of 3, making it easy to reference for quick calculations!

Multiples of 3 by Repeated Addition

Another way to understand multiples of 3 is through repeated addition. Instead of multiplying, you can add 3 repeatedly to generate the multiples. For example:

• Start with 0: 0+3=3
• Add 3 again: 3+3=6
• Continue this process: 6+3=9, 9+3=12, 12+3=15, 15+3=18, 18+3=21

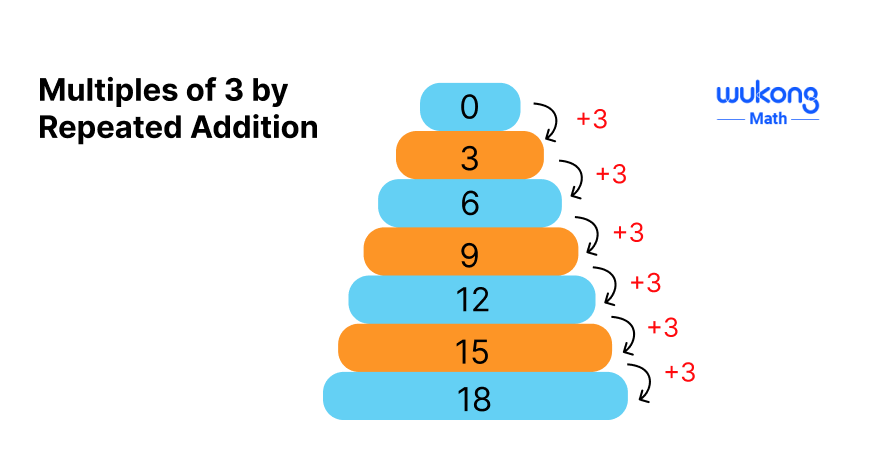
This method shows how each multiple of 3 is simply the previous multiple plus 3. It emphasizes the pattern and structure of the sequence, making it easier to visualize the concept of multiples. This sequence is a multiple of 3, illustrating how each number in the sequence is derived by adding 3 to the previous number.

Properties of Multiples of 3

Multiples of 3 have several interesting properties that make them useful in various mathematical applications. Understanding these properties can help you recognize patterns and solve problems more efficiently.

Is 0 a Multiple of 3?

Yes, 0 is a multiple of 3. In fact, 0 is a multiple of every number, including 3. This is because 0 can be divided by any number without leaving a remainder. For example, 0 ÷ 3 = 0, which means 0 is a multiple of 3.

Are the Multiples of 3 Always Odd or Even?

No, the multiples of 3 are not always odd or even. When 3 is multiplied by an even number, the product is even, and when 3 is multiplied by an odd number, the product is odd. When 3 is multiplied by an odd number, the product is odd because 3 times an odd number results in an odd product. For example:

• 3 × 2 = 6 (even)
• 3 × 3 = 9 (odd)

This pattern continues indefinitely, showing that multiples of 3 can be either odd or even depending on the number they are multiplied by.

To provide a clearer picture, here are the multiples of 3 up to 80 and 100.

Odd and Even Multiples of 3

Multiples of 3 can be classified into odd and even numbers:

• Odd Multiples of 3: These are numbers like 3, 9, 15, etc. They are not divisible by 2, meaning they leave a remainder when divided by 2. When there is an odd number of threes, there are leftover elements that cannot be paired, resulting in an additional unpaired group.
• Even Multiples of 3: These include numbers like 6, 12, 18, etc. These are divisible by 2 without any remainder.

In summary, the multiples of 3 consist of both odd and even integers, demonstrating the diversity within this series of numbers.

Solved Examples on Multiples of 3

This task investigates divisibility properties of multiples of 3.

Example 1: Determine if a Number is a Multiple of 3

Question: Is 45 a multiple of 3? Answer: Yes, 45 is a multiple of 3. Explanation: To determine if 45 is a multiple of 3, divide it by 3: 45÷3=15 (no remainder). Since there is no remainder value, 45 is a multiple of 3.

Example 2: Find the Next Multiple of 3

Question: What is the next multiple of 3 after 32?
Answer: The next multiple of 3 is 33.
Explanation: Start from 32 and find the smallest number greater than 32 that is divisible by 3.

32÷3=10.67 (not a whole number).

The next whole number is 11:
3×11=33
Thus, the next multiple of 3 after 32 is 33.

---

Example 3: Identify Multiples of 3 in a Range

Question: List all the multiples of 3 between 10 and 30.
Answer: The multiples of 3 between 10 and 30 are 12, 15, 18, 21, 24, 27, and 30.
Explanation: Start from the nearest multiple of 3 greater than 10, which is 12, and continue adding 3 until reaching 30:

• 12, 15, 18, 21, 24, 27, 30.

---

Example 4: Sum of Multiples of 3

Question: What is the sum of the first five multiples of 3?
Answer: The sum is 45.
Explanation: The first five multiples of 3 are 3, 6, 9, 12, and 15. Calculate the sum:
3+6+9+12+15=45.3 + 6 + 9 + 12 + 15 = 45.3+6+9+12+15=45.

---

Example 5: Find a Multiple of 3 within a Specific Range

Question: What is the largest multiple of 3 less than 50?
Answer: The largest multiple of 3 less than 50 is 48.
Explanation: The multiples of 3 less than 50 are:
0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48.
The largest one is 48.

---

Interactive Questions on Multiples of 3

Question 1:

Which of the following numbers is a multiple of 3?
A) 14
B) 18
C) 22
D) 25

Answer: B) 18

---

Question 2:

What is the first multiple of 3 greater than 20?
A) 21
B) 23
C) 24
D) 27

Answer: A) 21

---

Question 3:

Which of the following is NOT a multiple of 3?
A) 27
B) 30
C) 35
D) 42

Answer: C) 35

---

Question 4:

What are the first three multiples of 3?
A) 1, 2, 3
B) 3, 6, 9
C) 3, 4, 5
D) 6, 9, 12

Answer: B) 3, 6, 9

---

Question 5:

Which of the following statements is true? A) All multiples of 3 are even. B) 0 is a multiple of 3. C) The number 10 is a multiple of 3. D) There are no odd multiples of 3.

Answer: B) 0 is a multiple of 3.

Explain why 0 is a multiple of 3, encouraging a deeper examination of the properties of multiples.

Real-World Applications of Multiples of 3

Previously, we discussed methods for finding common multiples and their importance in real-world applications.

Multiples of 3 have numerous real-world applications in various fields, including science, technology, engineering, and mathematics (STEM). Understanding how to use multiples of 3 can make everyday tasks easier and more efficient.

Multiples of 3 are used in many everyday situations, such as:

• Measuring ingredients for cooking: When a recipe calls for 3 cups of flour, you can easily multiply this by 2 or 3 to get 6 or 9 cups.
• Counting money: When you have $3 bills, you can easily count them in multiples of 3 to get $6, $9, or $12.
• Building design: Architects often use multiples of 3 when designing buildings to create symmetrical and aesthetically pleasing structures.
• Music: Musicians use multiples of 3 when composing music to create rhythmic patterns and harmonies.

In conclusion, multiples of 3 are an essential concept in mathematics with numerous real-world applications. Understanding the properties of multiples of 3 can help you solve problems and make calculations more efficient.

Frequently Asked Questions

Q 1. Multiples of 3 up to 80:

0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78.

Q 2. What is the least common multiple of 7 and 3?

A: The least common multiple (LCM) of 7 and 3 is 21.

Q 4. What is the smallest common multiple of 3 and 4?

A: The smallest common multiple of 3 and 4 is 12.

Q 5. Are multiples of 3 always multiples of 6?

A: Yes, every multiple of 6 is also a multiple of 3, but not every multiple of 3 is a multiple of 6. Similarly, while multiples of 6 are also multiples of 3, they are not necessarily multiples of 7.

Q 6. What is the first ten multiples of 3?

A: The first ten multiples of 3 are 0, 3, 6, 9, 12, 15, 18, 21, 24, and 27.

Q 7. What are the multiples of 3 between 100 and 1000?

A: The multiples of 3 between 100 and 1000 include 102, 105, 108, …, up to 999.

Q 8. What is the sum of first five multiples of 3?

To find the sum of the first five multiples of 3, we first identify them:

• 3 × 1 = 3
• 3 × 2 = 6
• 3 × 3 = 9
• 3 × 4 = 12
• 3 × 5 = 15

Now, we can sum these multiples: 3+6+9+12+15

Calculating this step by step:

• 3+6=9
• 9+9=18
• 18+12=30
• 30+15=45

Thus, the sum of the first five multiples of 3 is 45.

Conclusion

Understanding the multiples of 3 is essential for mastering basic mathematics. This article has provided a clear definition, methods for identifying multiples, and practical examples to enhance your learning. By grasping these concepts, you not only improve your mathematical skills but also build a solid foundation for tackling more advanced topics. If you’re eager to dive deeper into difference in the multiples or enhance your skills further, consider enrolling in WuKong Math courses. Their structured programs can provide you with the guidance and practice needed to excel in mathematics.