Multiples of 7 – All the Multiples of 7 up to 1000

What are the multiples of 7?
Quick calculation: A number is a multiple of 7 if it equals 7 × any whole number (e.g., 7 × 1 = 7, 7 × 2 = 14, 7 × 3 = 21, 7 × 4 = 28, 7 × 5 = 35, and so on).
To check quickly, divide the number by 7 — if the result is a whole number with no remainder, it’s a multiple of 7.

This article includes a convenient multiples of 7 calculator — just enter any number or range and get an instant list of multiples.

Understanding multiples of 7 is a key skill in the U.S. Common Core State Standards for Mathematics, covered in 4th grade math under Operations & Algebraic Thinking (standard 4.OA.B.4). Students learn to determine whether a whole number is a multiple of a given one-digit number, recognize the relationship between factors and multiples, and apply them to solve real-world problems.

If you are interested in numbers, you might want to learn how to express these numbers in Chinese.

What are Multiples of 7?

Multiples of 7 are numbers that leave no remainder when divided by 7. In other words, any number that’s evenly divisible by 7 is a multiple of 7. There are an infinite number of multiples of 7 because you can multiply 7 by any integer, positive integers, negative integers, and zero. Formally, multiples of 7 can be written as 7 × n, where “n”  is any integer

For example, multiplying 7 by the integers 1 through 14 gives the first 14 positive multiples of 7. These include 7, 14, 21, 28, 35, 42, and so on, as shown in the image below:

Multiples of 7 Online Calculator

List of Multiples of 7

The following table lists 20 infinite multiples of 7 by multiplication:

In general, for two values, a and b, b is a multiple of a if b = a * n.

What Are all the Multiples of 7 up to 1000?

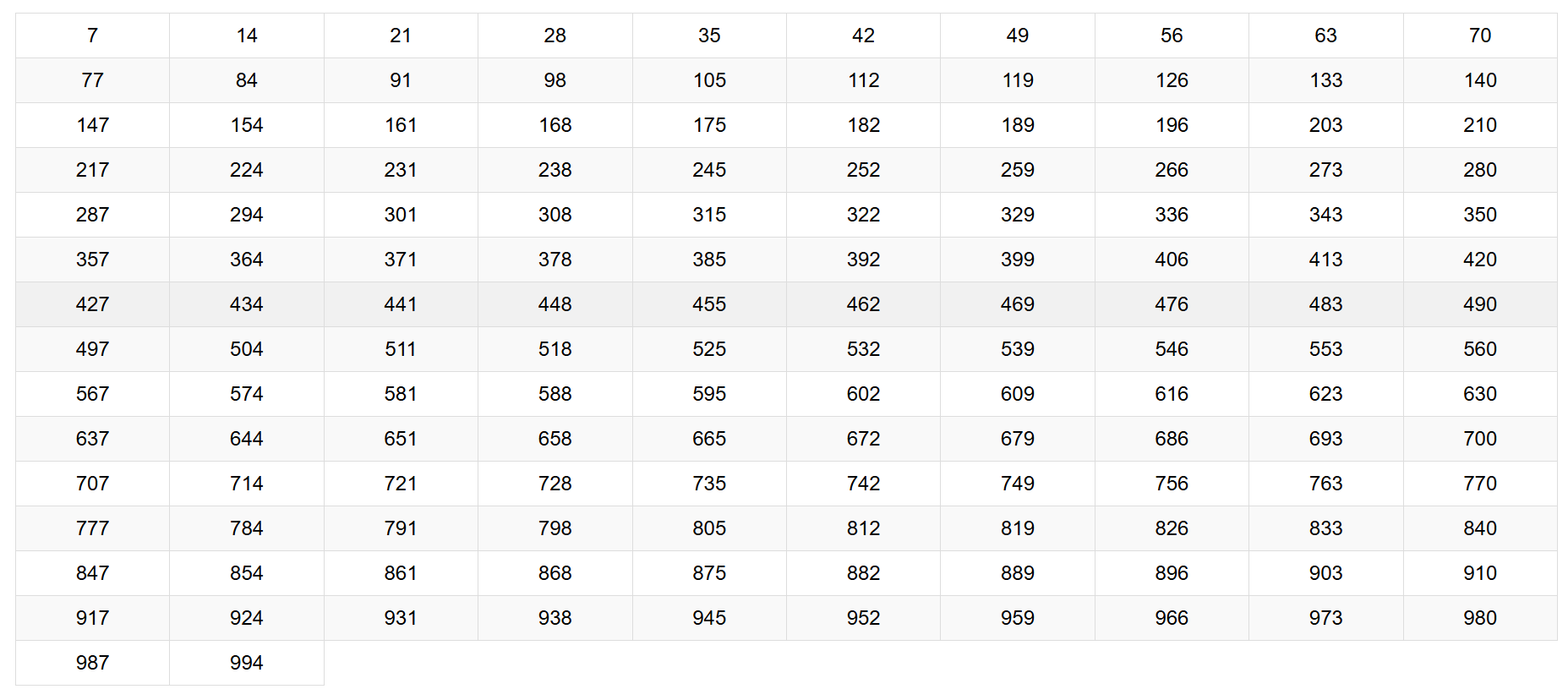
The multiples of 7 up to 1000 are: 7, 14, 21, 28, 35, …, 994. These numbers are all divisible by 7 without leaving a remainder. Each multiple is obtained by multiplying 7 by a whole number, illustrating how multiplication can be used to identify factors within a specific range. Below is a complete table of all the multiples of 7 up to 1000:

This format allows for an easy overview of the multiples of 7 up to 1000.

How many Multiples of 7 are there between 100 and 1000?

There are 128 multiples of 7 between 100 and 1000.

To see how this is calculated:

• Step 1. Identifying the smallest multiple of 7 greater than or equal to 100: 100 ÷ 7 ≈ 15

Rounding upwards gives 15, so the smallest multiple of 7 is: 15 x 7 = 105
（Smallest multiple ≥ 100: 100 ÷ 7 ≈ 15 → 15 × 7 = 105）

• Step 2. Identifying the largest multiple of 7 less than or equal to 1000: 1000 ÷ 7 ≈ 142

Rounding down gives 142, so the largest multiple of 7 is: 142 x 7 = 994
（Largest multiple ≤ 1000: 1000 ÷ 7 ≈ 142 → 142 × 7 = 994）

• Step 3. Counting numbers of the multiples of 7 from 105 to 994: 105, 112, 119, 126, 133, 140, ..., 994

The common difference of this sequence of numbers is 7, the first term is 105 and the last is 994. The method for finding the number of terms: n = (994-105) ÷ 7 + 1 = 128
（Count the multiples: The sequence is 105, 112, 119, …, 994.）

Thus, there are 128 multiples of 7 between 100 and 1000.

What are the Least Common Multiples of 7?

The least common multiple (LCM) of 7 and another number is the smallest number that is divisible by both 7 and that number.

Since 7 is a prime number, the LCM of 7 and any other number n is simply 7 × n (unless "n" is a multiple of 7).

If you are looking for the least common multiples of 7 with other numbers, here are a few examples:

• LCM(7, 1) = 7
• LCM(7, 2) = 14
• LCM(7, 3) = 21
• LCM(7, 4) = 28
• LCM(7, 5) = 35
• LCM(7, 6) = 42
• LCM(7, 8) = 56
• LCM(7, 9) = 63
• LCM(7, 10) = 70

And so on, with each LCM being a multiple of 7.

Solved Examples on Multiples of 7

Here are some examples of solved problems that provide answers to common questions about multiples of 7:

Q.1: What is the average of the first ten multiples of 7?

Answer: The average of the first ten multiples of 7 is equal to the sum of all multiples divided by 10.

Average = (7+14+21+28+35+42+49+56+63+70) ÷ 10

= 385 ÷ 10

= 38.5

Therefore, the required average is 38.5.

Q.2: Is 72 a multiple of 7 yes, or no?

Answer: No, 72 is not a 7 multiple. It is not multiple, as when divided by 7, it will leave a remainder of 2.

Q.3: What are the multiples of 7 that are less than 40?

Answer: The multiples of natural number 7, which are less than 40 are 7, 14, 21, 28, 35.

Q.4: What is the least common multiple of 6 and 7?

Answer: To find the least common multiple of 6 and 7, first we will write the multiples of each of the numbers.

• Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
• Multiples of 7 = 7, 14, 21, 28, 35, 42, 49, 56, 63, 70

Therefore, we can see, the LCM of 6 and 7 is 42.

How to explain multiples of 7 simply to a child？

The easiest way to explain multiples of 7 is to use things children already know. Here are three simple methods:

• The "Calendar" Method: This is the best way! Tell them that multiples of 7 are just "full weeks." 1 week is 7 days, 2 weeks are 14 days, and 3 weeks are 21 days. Every time a week passes, you’ve hit a multiple of 7.
• The "Frog Leap" Story: Imagine a frog that only jumps 7 steps at a time. Every spot where the frog lands is a multiple.
  • First jump: 7
  • Second jump: 14
  • Third jump: 21
• The "Snow White" Rule: If Snow White has 1 group of Seven Dwarfs, she has 7 friends. If there were 2 groups of Seven Dwarfs, she would have 14 friends. Each new group adds another multiple of 7.

How many multiples of 7 are in 100?

There are 14 multiples of 7 that fit inside 100.

To find this, you can use a simple division:

• 100÷7=14100÷7=14 with a remainder of 22.

This means the number 7 can fit into 100 exactly 14 times. If you try to find the 15th multiple (7×157×15), you get 105, which is too big for our 100 limit.

The list inside 100 is: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, and 98.

What are the multiples of 7 up to 150?

Here is the complete list of multiples of 7, organized to make them easy to read:

The first 10 (1-70):
7, 14, 21, 28, 35, 42, 49, 56, 63, 70

The next 10 (71-140):
77, 84, 91, 98, 105, 112, 119, 126, 133, 140

The final one under 150:
147

(The next one would be 154, which is over the 150 limit.)

Multiplication Tables

Multiplication Tables From 1-24

This collection of multiplication resources is designed to support mastery of Common Core State Standards for Operations and Algebraic Thinking. Specifically, it aligns with CCSS.MATH.CONTENT.3.OA.C.7, which requires students to fluently multiply and divide within 100, and 4.OA.B.4, focusing on factors and multiples. By exploring these tables, learners develop the algebraic foundation necessary for mental math fluency and higher-level problem solving.

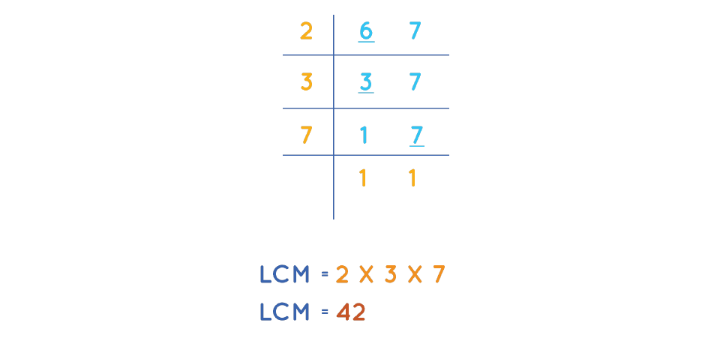
FAQs on Multiples of 7

Nathan | WuKong Math Teacher

Nathan, a graduate of the University of New South Wales, brings over 9 years of expertise in teaching Mathematics and Science across primary and secondary levels. Known for his rigorous yet steady instructional style, Nathan has earned high acclaim from students in grades 1-12. He is widely recognized for his unique ability to blend academic rigor with engaging, interactive lessons, making complex concepts accessible and fun for every student.