Odd Numbers: Definition, Properties, 1 to 100 List, Worksheets

Have you ever wondered what makes a number odd? Understanding odd numbers is essential for students and educators alike, especially in elementary mathematics.

This guide aims to provide a comprehensive overview of odd numbers, exploring their definition, properties, and types while also delving into practical examples and solved problems. By the end of this article, you will have a firm grasp of what odd numbers are and how to identify and work with them effectively.

Part 1: What Are Odd Numbers?

Odd numbers are integers that cannot be divided evenly by 2. In simpler terms, when you divide an odd number by 2, you will always leave a remainder of 1, meaning they are not divisible by 2. This characteristic makes odd numbers distinct from even numbers, which can be divided by 2 without any remainder.

Definition and Meaning of Odd Numbers

Odd numbers are integers that cannot be divided by 2 without leaving a remainder. In other words, an odd number is always 1 more or 1 less than an even number. The sequence of odd numbers starts from 1 and continues indefinitely: 1, 3, 5, 7, 9, 11, and so on. These numbers are unique because they do not fit into pairs, making them distinct from even numbers. Odd numbers are also known as gnomonic numbers, a term that highlights their unique properties in mathematics.

Examples of Odd Numbers

Let’s take a look at a few odd numbers like 3, 5, and 7:

• 1: Odd (1 ÷ 2 = 0 remainder 1)
• 3: Odd (3 ÷ 2 = 1 remainder 1)
• 5: Odd (5 ÷ 2 = 2 remainder 1)
• 7: Odd (7 ÷ 2 = 3 remainder 1)

To help visualize the concept, consider the example of apples. If you have 5 apples, you cannot pair them up completely without having one apple left over. This visual representation can make it easier to understand why these numbers are classified as odd.

Characteristics of Odd Numbers

• Last Digit: Odd numbers end with the digits 1, 3, 5, 7, or 9.
• Divisibility: They cannot be divided equally into two parts, which is why one apple remains unpaired.
• Range: Odd numbers can be both positive and negative, meaning numbers like -1, -3, and -5 are also odd.

Part 2: Even and Odd Numbers

Understanding the relationship between an even or odd number is fundamental in mathematics.

• Even Numbers: These are integers that can be divided evenly by 2. They end with 0, 2, 4, 6, or 8. For instance, numbers like 2, 4, 6, and 8 are even.
• Odd Numbers: As mentioned earlier, odd numbers cannot be divided evenly by 2 and end with 1, 3, 5, 7, or 9.

How to Identify Even or Odd Numbers

To determine if a number is even or odd:

1. Look at the Last Digit:

• If the last digit is 0, 2, 4, 6, or 8, it’s even.
• If the last digit is 1, 3, 5, 7, or 9, it’s odd.

This method is based on the divisibility rule, which helps in identifying even and odd numbers.

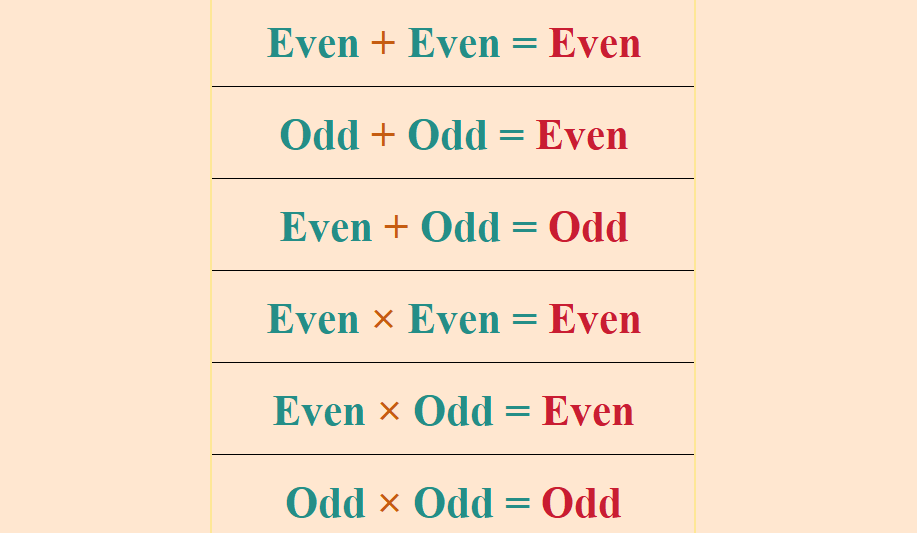
Identifying Odd Numbers

To identify an odd number, you can use the following methods:

1. Check the Last Digit: If the number ends in 1, 3, 5, 7, or 9, it’s an odd number.
2. Divide by 2: Try dividing the number by 2. If it leaves a remainder of 1, it’s an odd number.
3. Compare with Even Numbers: Check if the number is 1 more or 1 less than an even number. If it is, it’s an odd number.

For example, the number 23 is an odd number because it ends in 3, cannot be divided by 2 without leaving a remainder, and is 1 more than the even number 22. These simple checks can help you quickly determine whether a number is odd or even.

Practical Application

This understanding is not just theoretical. It can be applied in real-world scenarios, such as sorting items or distributing snacks. For example, if you have 12 cookies and want to share them with 4 friends, you can give each friend 3 cookies. But if you have 13 cookies, one cookie will remain.

Part 3: List of Odd Numbers (1 to 100)

Let’s explore the first few odd numbers like 1, 3, 5, 7, 9, 11, 13, 15, 17, and 19. Let’s explore all the odd numbers from 1 to 100. Here’s a table listing the odd numbers from 1 to 100 in four columns:

Odd Numbers	Odd Numbers	Odd Numbers	Odd Numbers
1	26	51	76
3	27	53	77
5	29	55	79
7	31	57	81
9	33	59	83
11	35	61	85
13	37	63	87
15	39	65	89
17	41	67	91
19	43	69	93
21	45	71	95
23	47	73	97
25	49	75	99

How Many Odd Numbers Are There?

In total, there are 50 odd numbers between 1 and 100. This is half of the total integers in that range, as they alternate with even numbers.

What are all the odd numbers?

The list of all odd numbers is infinite, but here are the first few odd numbers:

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, …

In general, odd numbers can be expressed in the form 2n+1, where nnn is any non-negative integer. This means that odd numbers continue indefinitely in both the positive and negative directions, such as -1, -3, -5, and so on.

Part 4: Types of Odd Numbers

Composite numbers are positive integers that have factors other than 1 and themselves; examples include 9, 15, and 21.

Odd numbers can be categorized into different types, which can be crucial for understanding their applications in various mathematical contexts.

1. Consecutive Odd Numbers

Consecutive odd numbers are odd numbers that follow each other in sequence, with a difference of 2 between them. For example:

• If nnn is an odd number, then nnn and n+2 are consecutive odd numbers.
• Examples include 3 and 5, 15 and 17, and so on.

2. Composite Odd Numbers

Composite odd numbers have factors other than 1 and themselves. Examples include:

• 9: (3 × 3)
• 15: (3 × 5)
• 21: (3 × 7)

Smallest Odd Composite Number

The smallest odd composite number is 9. Among the odd numbers, 1 is neither prime nor composite, while 3, 5, and 7 are prime. Thus, 9 is the first composite odd number.

Part 5: Properties of Odd Numbers

Understanding the properties of odd numbers helps in solving various mathematical problems effectively. The following points outline the properties of odd numbers:

Properties of Addition

• Odd + Odd = Even: For example, 3 + 5 = 8 (even).
• Even + Odd = Odd: For example, 6 + 1 = 7 (odd).

Properties of Subtraction

• Even – Odd = Odd: For example, 10 – 5 = 5 (odd).
• Odd – Odd = Even: For example, 11 – 3 = 8 (even).

Properties of Multiplication

• Odd × Odd = Odd: For example, 3 × 5 = 15 (odd).
• Even × Odd = Even: For example, 4 × 3 = 12 (even).

Properties of Division

• When dividing two odd numbers, if the denominator is a factor of the numerator, the result is an odd number. For example, 9 ÷ 3 = 3 (odd).
• If the denominator is not a factor, the result is a decimal.

Part 6: Solved Examples on Odd Numbers

Let’s walk through some solved examples to reinforce these concepts. Here is an odd numbers example to demonstrate various properties and calculations.

Example 1: Find the Sum of the Smallest and Largest 3-Digit Odd Numbers

• Smallest 3-digit odd number: 101
• Largest 3-digit odd number: 999
• Sum: 101 + 999 = 1100 (which is even).

Example 2: Determine if 135 is Odd or Even

To check:

• Divide 135 by 2: 135 ÷ 2 = 67 remainder 1.
• Since there is a remainder, 135 is an odd number.

Example 3: Find the Next Three Odd Numbers After 23

• Start with 23:
• Next odd numbers: 25, 27, and 29.

Example 4: Find Two Consecutive Odd Numbers Whose Sum is 144

Let x be the first odd number.

• Then x+(x+2)=144
• Simplifying gives 2x+2=144, so 2x=142, thus x=71.
• The two consecutive odd numbers are 71 and 73.

Example 5: How to Determine if a Number is Odd or Even

To determine if a number is odd or even:

• Check the last digit.
• If the last digit is 1, 3, 5, 7, or 9, then the number is odd.
• If the last digit is 0, 2, 4, 6, or 8, then the number is even.

Odd Numbers Worksheet: Download for Free

There is a worksheet that can help you reinforce these concepts. You can download the printable math worksheets PDF now.

Resources and Practice

To practice identifying odd numbers, you can try the following exercises:

1. Write Down Odd Numbers: Write down the first 20 odd numbers and check if they meet the criteria for being odd.
2. Divide by 2: Try dividing a list of numbers by 2 and identify which ones leave a remainder of 1.
3. Use a Number Line: Create a number line with even and odd numbers marked and practice identifying the odd numbers.

You can also use online resources such as math games, quizzes, and worksheets to practice identifying odd numbers. Some recommended resources include:

• Khan Academy’s “Odd and Even Numbers” video: A comprehensive video explaining the concept of odd and even numbers.
• Math Playground’s “Odd and Even Numbers” interactive game: An engaging game to practice identifying odd and even numbers.
• IXL’s “Odd and Even Numbers” practice worksheet: A worksheet to reinforce your understanding through practice.

These resources can provide additional support and interactive ways to master the concept of odd numbers.

FAQs on Odd Numbers

Q1: Is Zero an Odd Number?

No, zero is an even number because it can be divided evenly by 2.

Q2: Are All Prime Numbers Odd?

No, the only even prime number is 2. All other prime numbers are odd.

Q3: What is the General Form of an Odd Number?

The general form of odd numbers can be expressed as 2n + 1, where n is any integer.

Q4: Find the First Ten Odd Numbers

The first ten odd numbers are: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19.

Q5: Is 2 an Odd Number?

No, 2 is an even number.

Q6: Is 15 Odd or Even?

15 is an odd number because it cannot be divided evenly by 2.

Q7: What are applications of the odd numbers？

Odd numbers have a variety of applications in mathematics and other fields. For example:

• In number theory, odd numbers are used to study prime numbers and other types of special numbers.
• In computer science, odd numbers are used to represent bits and other types of data.
• In physics, odd numbers are used to describe the behavior of subatomic particles.

Conclusion

In this article, we explored the definition, properties, and types of odd numbers. Understanding these concepts is essential for anyone studying mathematics. With solid knowledge of odd numbers, you can tackle various mathematical problems confidently. For additional practice and learning, consider exploring worksheets and engaging with interactive math online classes.